Вот наткнулся на одну интересную статейку.
Если будет время прочитайте. Интересно!
Мощность vs Момент
Тяга
Тяга - это сила, которая заставляет ваш автомобиль двигаться вперед. Не имеет значения, сколько крутящего момента ваш двигатель создает, на какой передаче вы едите, насколько велики ваши колеса, как блестит ваш глушитель, или как много наклеек у вас на двери - тяга определяет, насколько быстро ваш автомобиль может ускоряться. В гонках, ускорение это то, что действительно имеет значение, и есть всего несколько способов заставить ваш автомобиль разгоняться быстрее:
ΣF = ma
В случае, если ΣF = сумма сил, действующих на автомобиль
m = масса автомобиля
a = ускорение автомобиля
Если вы хотите улучшить ускорение, необходимо уменьшить вес, увеличить тягу, или уменьшить другие силы, которые выступают против тяги.
Крутящий момент
Крутящий момент - это сила, приложенная к плечу. Вместо того, чтобы думать, что это сила, которая заставляет дигаться вперед, лучше представить, что это сила, которая заставляет вращаться что либо. Ежели я приложу силу к определенной точке, то крутящим моментом будет расстояние до точки, умноженное на часть силы, перпендикулярно приложенной к этому расстоянию (тут я мог накосячить, коррект ми иф айм вронг, как грица).
Уравнение для расчета крутящего момента:
τ = Fd
Где, τ = крутящий момент
F = часть полной силы, действующей перпендикулярно вектора расстояния
D = расстояние между опорой и точкой, в которой сила F прикладывается
Следует отметить, что крутящий момент происходит мгновенно.
Работа
Работа - это энергия, которая используется для перемещения объекта. Усилия и момент могут существовать всегда, но пока объект не переместился, никакая работа не была выполнена. Если я пытаюсь переместить объект, но я не могу сдвинуть его с места, то я не выполняю никакой работы. Я использую много энергии, чтобы развивать силу, но он используется для создания тепла, а не для выполнения работы. Как только объект двигается, то часть энергии уходит на выполнение работы. Уравнение, используемое для определения работы, выполняемой на объект:
W = Fx
Где, W = выполненной работы
F = сила, приложенная к объекту
х = смещение объекта
Работа также может быть выполнена на вращающийся объект, например коленчатым валом. Уравнение в этом случае немного отличается:
W = τθ
Где, W = выполненной работы
τ = крутящий момент
θ = угловое смещение (в радианах)
Вместо силы используется крутящий момент, а смещение выражается в радианах вместо футов или метров. Если объект совершает один оборот, его угловое смещение 2π радиан (или 360 °), если это делает ¼ оборот, его угловое смещение π / 2 радиан (или 90 °) и т.д. На основе этого уравнения, должно быть очевидно что крутящий момент не является показателем работы. Если прикладывается крутящий момент на валу, но он не вращается, никакая работа не выполняется. Это кажется немного запутанным, поскольку оба имеют одинаковые единицы, но они не измеряют те же величины.
Мощность
Мощность является мерой того, сколько работы выполняется за единицу времени. Она не измеряется количеством приложенного крутящего момента, а только выполненную работу. Для двигателей, используется величина под названием "лошадиная сила". Если двигатель мощностью 1 л.с., то он может выполнять 550 ft-lb работы (не момента) каждую секунду. Не имеет значения, производится 1 ft-lb крутящего момента или 100 ft-lb крутящего момента.
Уравнение для измерения мощности:
P = FV
Где, P = мощность
F = приложенной силы
V = скорость, при которой приложена сила
Для вращающегося объекта, это:
P = τω
Где, P = мощность
τ = крутящий момент
ω = скорость вращения, при которой прикладывается крутящий момент
Для двигателей, которые мы привыкли видеть, уравнение: Мощность = (крутящий момент) * (об/мин)/5252
Однако то, что это действительно означает? Где взялись 5252?
Расчет Лошадиных сил
Как уже упоминалось, мощность может быть рассчитана путем умножения крутящего момента, приложенного к вращающемуся объекту на скорость, с которой он вращается. Тем не менее, базовая единица для скорости вращения задается в радианах в секунду, а мы обычно измерять частоту вращения двигателя в оборотах в минуту. Поэтому, если мы хотим использовать обороты в минуту, то мы должны преобразовать эту веkичину. Так как мы имем 2π радиан за один оборот, и 60 секунд в течение одной минуты, мы должны разделить на 60 и умножить на 2π:
P = (крутящий момент) * (RPM) * (1 мин / 60 с) * (2π рад / 1 оборот) = 2π * (крутящий момент) * (об / мин) 60
Далее, мы хотим увидеть мощность, выраженную в лошадиных силах, а не ft-lb/s. Таким образом, мы должны разделить на 550:
Мощность = 2π * (крутящий момент) * (RPM) / (60 * 550) = 2π * (крутящий момент) * (об / мин) 33000
С 33000/2π составляет около 5252, мы просто используем: Мощность = (крутящий момент) * (об / мин)/ 5252
Теперь мы видим, что это не просто случайные уравнения с бессмысленным результатом. Это мера скорости, с которой производится энергия и скорость, с которой выполняется работа.
Ну и что?
К настоящему времени, вы, вероятно, устали от моих уроков физики, поэтому я буду двигаться дальше. Как мы можем использовать эту информацию для разработки наших двигателей? Хотим ли мы, производить тонну крутящего момента, как дизельный двигатель или кучу лошадиных сил, как двигатель мотоцикла? Давайте рассмотрим несколько примеров.
У одной известной конторы я нашел док-ы, которые содержит результаты трех различных двигателей: B16A, D16A6, и B18A. Я оцифрованных кривые и воссоздал их для вас:
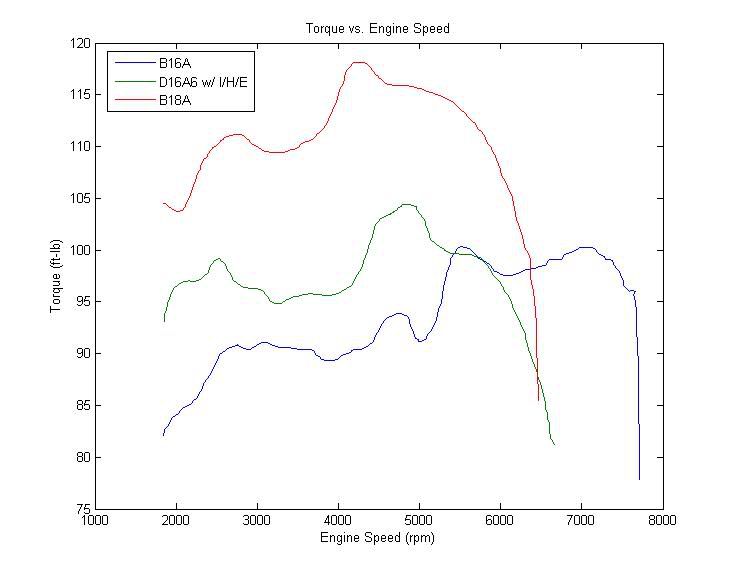
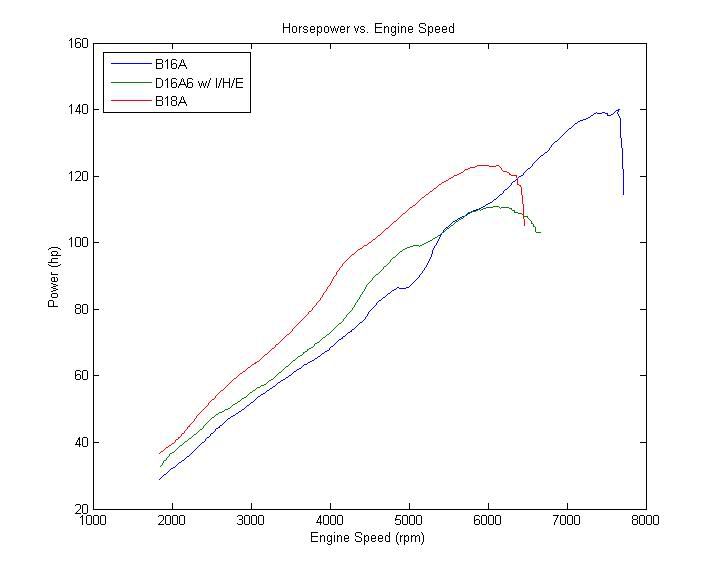
Как видно из графиков, B16A производит 100,3 ft-lb крутящего момента и 140,1 л.с. на колесах, D16A6 производит, 104,5 ft-lb крутящего момента и 110,9 л.с. на колесах, и B18A производит 118,1 ft-lb крутящего момента и 123,3 л.с. на колесах. Как и ожидалось, b16a показывает меньший крутящий момент, но больше лошадиных сил, B18A делает больше крутящего момента, а D16A6 делает меньше лошадиных сил. Эти кривые полезны сами по себе, но они не говорят нам ничего о тяге, которая является тем, о чем мы действительно заботимся. Итак, время подсчетов. Во-первых, мне нужно передаточные числа коробок, которые используются с этими двигателями:
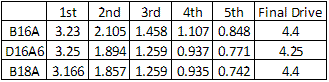
Учитывая, что все другие параметры одинаковые, мы можем выяснить, какой тягой будут обладать агрегаты на разных скоростях.
Тем не менее, здесь есть одна проблема. На низких скоростях может быть слишком много тяги и шины не будут справляться, буксуя. Не вдаваясь в излишние подробности, тяговый предел автомобиля определяет его центр тяжести, вес, колесная база и шины. Когда машина трогается, эти факторы влияют на то, какой вес передается от передних колес к задним. Тем не менее, FWD автомобилей хотят получить столько нагрузки на ведущие колеса, сколько возможно, и перенос веса работает против них. Это приводит к их основным недостатком для дрэг-рейсинга. В этом примере, я предпологаю, что тяговые предел составляет около 610 кг для типичного Сивика со стритовыми шинами, что соответствует максимальным ускорением около 0,54 г.
Максимальное тяговое усилие
Когда все вышеперечисленные сведения объединяются, мы получаем график, подобный этому:
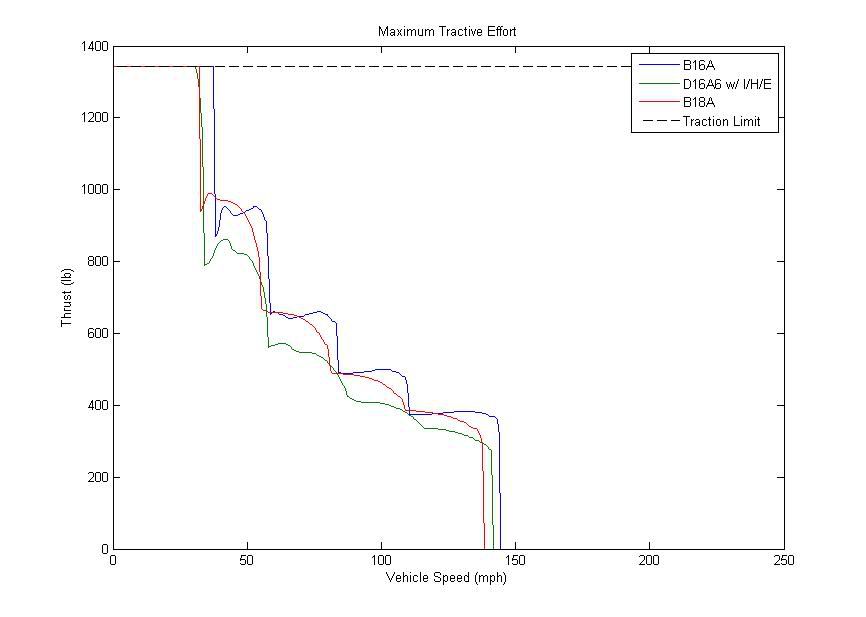
На этом графике мы видим какую тягу двигатель может производить на любой скорости. Обратите внимание, что ниже 30 миль/ч, все три двигателя производят 1344 фунтов тяги, так как автомобиль является тягово-ограниченным. Мы также видим, как тяга падает в конце каждой передачи. На основании результатов видим, что b16a производит в среднем 858,3 фунтов тяги от 0 до 120 миль / ч, D16A6 производит в среднем 774,5 фунтов, а B18A производит в среднем 821,8 фунтов. Поскольку мы используем то же сопротивление и вес в каждом случае, ускорение каждого автомобиля будет следовать этим тенденциям. Это означает, что B16A (в среднем) 4% быстрее, чем B18A и 11% быстрее, чем D16A6.
Почему D16A6 показал гораздо меньше тяги?
Давайте внимательнее посмотрим на кривую для D16A6. Вы заметите, что ось х скорости автомобиля, а ось у - тяга. Если вы помните, ранее в этой статье, произведение скорости и тяги - это мощность. Если двигатель может производить только 110,9 л.с. на колесах (как D16A6), то произведение скорости транспортного средства, и тяги никогда не может быть больше, чем 110,9 лошадиных сил. В то время как крутящий момент двигателя манипулируют передач и размер шин, мощность остается постоянной (без учета трения трансмиссии). Теперь, давайте построим кривую для D16A6, отображающую предел мощности. Я включил B16A кривой для сравнения:
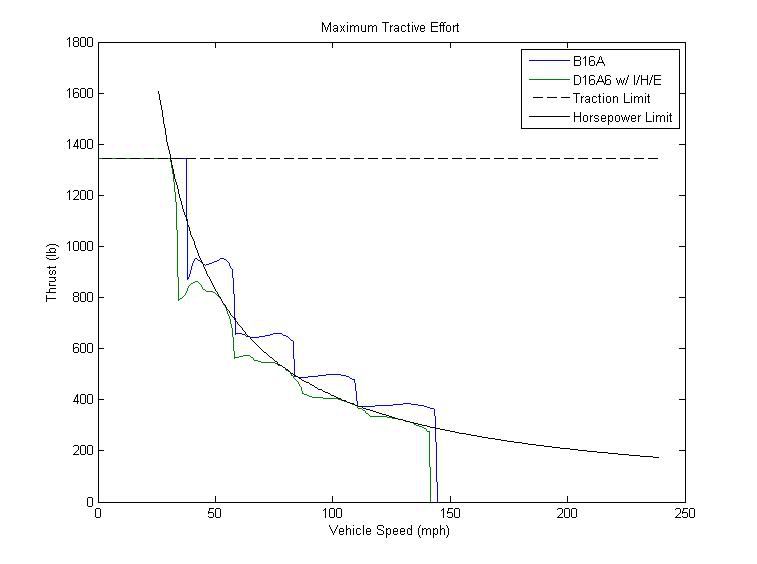
Видим, что кривая D16A6 касается его предела лошадиных сил пять раз - по разу на каждой передаче. Эти точки появляются на пиках, когда мотор производит больше всего л.с. Это точки, в которых машина быстрее всего разгоняется. Поэтому, если мы можем изменить кривую крутящего момента и/или передаточные числа таким образом, чтобы кривая тягового усилия стала ближе к пределу лошадиных сил, мы сможем производить больше средней тяги, и машина поедет быстрее.
Что, если D16A6 получит лучшую (более короткую - прим. ред.) коробку?
Справедливо. Давайте дадим B18A и D16A6 такую же коробку, как у Б16А:

В этом случае, B18A близок к B16A, и при прочих равных условиях, он будет только на 1% медленнее. Тем не менее, тяга B16A на 7% больше, чем тяга D16A6. Не имеет значения, какими коробками вы укомплектуете машины, D16A6 лососнет тунца, производя на 30whp меньше, чем B16A, хоть момента у последнего и меньше.
Итоги
Если вы хотите, чтобы ваш автомобиль был быстрее, вам нужно больше лошадей. Не имеет значения, строите вы машину Формулы 1, или стритовую гонку. В гонках, побеждает мощность. Если у вас есть обоснованй контраргумент, не стесняйтесь поделиться. В противном случае, пожалуйста, прекратите говорить "Лошадиная сила продает автомобили, но крутящий момент побеждает гонки".
Ну или добавлю от себя примерчик.
М3 Е36 с мотором 3,0 и 286 л.с. и моментом 320Нм
Хонда С2000 2 литра, 240 л.с. и 208 Нм
Разгон у М3 0-100 6 секунд, у С2000 6,2 сек
